如图小明从B点出发在河边挑水去给A点的小树浇水，怎样走路程最短。老师们教给我们的方法是：从A点做垂直于河边的线，在线上找到与A点到河边等距的A”点。连接 BA”之间的直线与河边的交点是取水点。但是孩子会问，老师是如何找到这一方法的呢？

方法一：折叠平面法

我们已知AB两点间直线距离最短。但过AB两点的直线不可能经过河边。

如果A点在河的对岸，则AB连线可以经过河边。其交点是取水点。

我们假想A点与河岸线确定的平面可以被分层（类似揭开三层的餐巾纸），将该平面的A点沿河岸线对翻到对岸，这样对岸有另一A点。

连接B点与河对岸的A点间直线距离最短。其与河岸线交点为取水点。

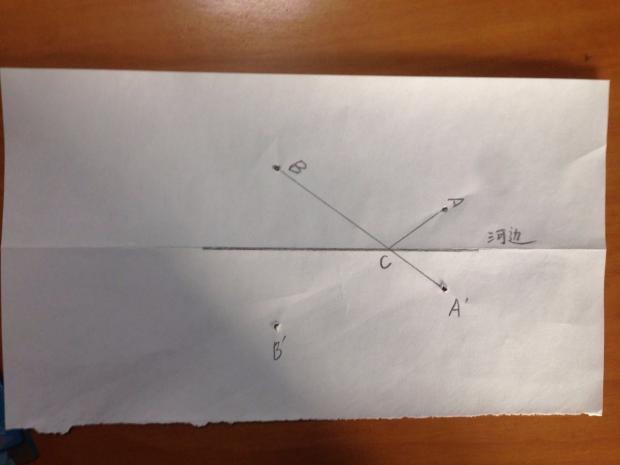
方法二：重力法

我们做一个实验，在书架上确定间隔开的高度不同的AB两点，在两点间连接一条较长的棉线，在棉线上挂重物。该重物会在重力作用下，找到棉线上最接近地面的一点C点。（我们将ABC平面上过C点平行于地面的线视为河边）

我们通过实验发现：

1）从C点将重物向左或者向右移动都会使棉线远离河边。因此C点是从A点经河边到B点的最短距离点。

2）AC、 BC 与河边线夹角相等。这一点是我们实验所得，也可以用力学分析加以证明。

分析：由于夹角相等，C点离A\B点在河边垂直点距离比等于A\B点到河边垂直距离比。（相似三角形原理）。通过测量A\B点到河边垂直距离可以找到河边的C点。

小结：

通过这道题的解答，我们了解到数学与人的想象力的关系，第一种方法我们通过想象“折叠平面”找到了解题思路。我们同时了解到数学与物理学之间的关系，第二种方法我们通过物理实验，找到解决数学题的思路。